tian27546 proposed a nice inequality and I give a proof.

Problem

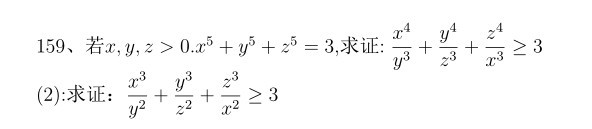
Proof
(1)by Holder inequality,
\[ \left(\sum{\frac{x^4}{y^3}}\right)^{5}\left(\sum{x^{10}y^5}\right)\left(\sum{x^5y^5}\right)^{2}\geq (\sum{x^5})^{8} \]
So,it's suffice to prove
\[ (\sum{x^5})^8\geq 3^{5}\left(\sum{x^{10}y^5}\right)\left(\sum{x^5y^5}\right)^{2} \]
We have the know result
\[ (\sum{a})^2\geq 3\sum{ab}\]
and
\[ (\sum{a})^5\geq 27(ab+bc+ca)(a^2b+b^2c+c^2a) \]
The result follows.
Done!

(2)
After homogenous,just need to check
\[ \left(\sum{\frac{x^3}{y^2}}\right)^5\geq 81(x^5+y^5+z^5) \]
recalling the Well-known Vasile Cirtoaje inequality
\[ \boxed{(a+b+c)^5\geq 81abc(a^2+b^2+c^2)} \]
and use $ a=\frac{x^3}{y^2},b=\frac{y^3}{z^2},c=\frac{y^3}{x^2}$,it's suffices to prove
\[ \frac{x^6}{y^4}+\frac{y^6}{z^4}+\frac{z^6}{x^4}\geq \frac{x^4}{yz}+\frac{y^4}{xz}+\frac{z^4}{xy} \]
Now,Using AM-GM inequality
\[26\frac{x^6}{y^4}+11\frac{y^6}{z^4}+\frac{z^6}{x^4}\geq 38\frac{x^4}{yz} \]
\[ 26\frac{y^6}{z^4}+11\frac{z^6}{x^4}+\frac{x^6}{y^4}\geq 38\frac{y^4}{xz} \]
\[26\frac{z^6}{x^4}+11\frac{x^6}{y^4}+\frac{y^6}{z^4}\geq 38\frac{z^4}{xy} \]
sum its up ,the result follows.
Done!

after a while.he also show the general one