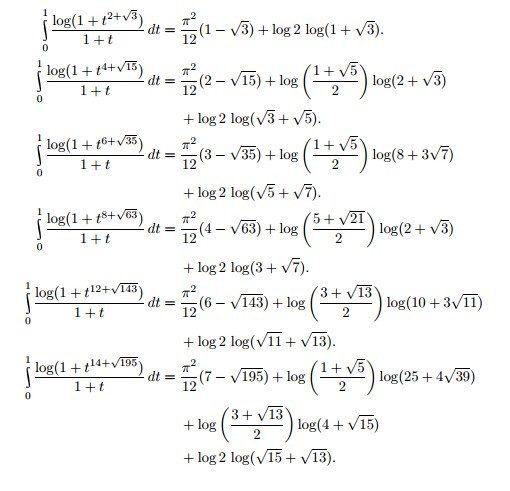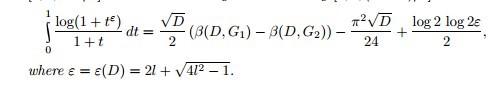陈洪葛的博客

设$f(x)$是正的递减的函数，证明

$$\int_{0}^{1}{xf(x)^2dx} \int_{0}^{1}{f(x)dx}\le \int_{0}^{1}{f(x)^2dx }\int_{0}^{1}{xf(x)dx}$$

证明 考虑

$$G(x,y)= \frac{1}{2}(x-y)(f(x)-f(y))f(x)f(y)$$

显然有

$$G(x,y)\leq 0$$

$$\iint_{[0,1]^{2}}{G(x,y)dxdy}=\int_{0}^{1}{xf^{2}(x)dx}\cdot \int_{0}^{1}{f(x)dx}-\int_{0}^{1}{xf(x)dx}\cdot\int_{0}^{1}{f^{2}(x)dx}$$

打开即得证

计算

$$\int_{0}^{\infty}{\frac{1}{\sqrt{x(1+e^{x})}}dx}$$

Solution

$$\begin{align} \int_0^\infty\frac{1}{\sqrt{x(1+e^x)}}\mathrm{d}x &=2\int_0^\infty\frac{1}{\sqrt{1+e^{x^2}}}\mathrm{d}x\\ &=2\int_0^\infty(1+e^{-x^2})^{-1/2}e^{-x^2/2}\;\mathrm{d}x\\ &=2\int_0^\infty\sum_{k=0}^\infty(-\tfrac{1}{4})^k\binom{2k}{k}e^{(2k+1)x^2/2}\;\mathrm{d}x\\ &=\sum_{k=0}^\infty(-\tfrac{1}{4})^k\binom{2k}{k}\sqrt{\frac{2\pi}{2k+1}} \end{align}$$

Mathematics StackExchange

据说还有

$$\displaystyle\lim\limits_{n\to\infty}\frac{1}{(2n-1)^{2011}}\sum_{k=0}^{n-1}\int_{2k\pi}^{(2k+1)\pi}x^{2010}\sin^3 x\cos^2 x \mathrm{d}x$$

(tian_275461)
解:
根据推广的积分第一中值定理，对每个正整数~$n~\exists\qquad \theta_n\in(0,1)$~使得
$$\begin{equation*}     \int_{2n\pi}^{(2n+1)\pi}x^{2010}\sin^3 x\cos^2 x \mathrm{d}x=     ((2n+\theta_n)\pi)^{2010}\int_{2n\pi}^{(2n+1)\pi}\sin^3 x\cos^2 x \mathrm{d}x \end{equation*}$$
由此得
$$\begin{align*} &\quad\int_{2n\pi}^{(2n+1)\pi}x^{2010}\sin^3 x\cos^2 x \mathrm{d}x\\ &=\left((2n\pi)^{2010}+o(n^{2010})\right)\int_{2n\pi}^{2n\pi+\pi}\sin^3 x\cos^2 x\mathrm{d}x\\ &=\left((2n\pi)^{2010}+o(n^{2010})\right)\left(\frac{\cos 5x}{80}-\frac{\cos 3x}{48}-\frac{\cos x}{8}\right)\Bigg|_{2n\pi}^{(2n+1)\pi}\\ &=\frac{4}{15}((2n\pi)^{2010}+o(n^{2010}))\qquad (n\to\infty) \end{align*}$$
另外
$$\begin{equation*}     (2n+1)^{2011}-(2n-1)^{2011}=4022(2n)^{2010}+o(n^{2010})\qquad (n\to\infty) \end{equation*}$$
根据~Stolz~定理
$$\begin{align*} &\quad\lim\limits_{n\to\infty}\frac{1}{(2n-1)^{2011}}\sum_{k=0}^{n-1}\int_{2k\pi}^{(2k+1)\pi}x^{2010}\sin^3 x\cos^2 x \mathrm{d}x\\ &=\lim_{n\to\infty}\frac{\displaystyle\int_{2n\pi}^{(2n+1)\pi}x^{2010}\sin^3 x\cos^2 x \mathrm{d}x}{ (2n+1)^{2011}-(2n-1)^{2011}}\\ &=\frac{2}{30165}\lim_{n\to \infty}\frac{(2n\pi)^{2010}+o(n^{2010})}{(2n)^{2010}+o(n^{2010})}\\ &=\frac{2\pi^{2010}}{30165} \end{align*}$$

此题的更一般结果为
$$\begin{equation*}     \lim_{n\to\infty}\frac{1}{(2n-1)^{p+1}}\sum_{k=0}^{n-1}\int_{2k\pi}^{(2k+1)\pi}x^p\sin^3 x\cos^2 x \mathrm{d}x =\frac{2\pi^p}{15(p+1)}(p>0) \end{equation*}$$

求极限
$$\displaystyle\lim_{n\to\infty}\frac{1+n+\frac{n^2}{2!}+\cdots+\frac{n^n}{n!}}{e^n}$$

（高等数学中的若干问题解析）
解： $$\begin{equation*}     e^n=1+n+\frac{n^2}{2!}+\cdots +\frac{n^n}{n!}+\frac{1}{n!}\int_0^n e^x(n-x)^n\mathrm{d}x \end{equation*}$$
原命题等价于
$$\begin{equation*}   \lim_{n\to\infty}\frac{e^{-n}}{n!}\int_0^n e^x(n-x)^n\mathrm{d}x=\frac{1}{2}\quad\text{而}      n!=\sqrt{2n\pi}(\frac{n}{e})^ne^{\frac{\theta}{12n}},\theta\in(0,1) \end{equation*}$$
$$\begin{equation*}    \Leftrightarrow \lim_{n\to\infty}\sqrt{n}\int_0^1[e^x(1-x)]^n\mathrm{d}x=\sqrt{\frac{\pi}{2}} \end{equation*}$$
注意到~$e^{-\frac{x^2}{2}}\geq(1-x)e^x (x\geq 0)$
$$\begin{equation*}    \therefore\qquad \overline{\lim_{n\to\infty}}\sqrt{n}\int_0^1[e^x(1-x)]^n\mathrm{d}x\leq     \overline{\lim_{n\to\infty}}\int_0^1\sqrt{n}e^{-\frac{nx^2}{2}}\mathrm{d}x=\sqrt{\frac{\pi}{2}} \end{equation*}$$
考虑
$$\begin{equation*}   f(x)=(1-x)e^x-e^{-\frac{ax^2}{2}}(x\geq 0,a\geq 1),f'(x)=xe^x(ae^{-\frac{ax^2}{2}-x}-1) \end{equation*}$$
$\displaystyle\because\quad \lim_{x\to 0^+}(ae^{-\frac{ax^2}{2}-x}-1)=a-1>0$，故存在$x_a\in(0,1)$，使得
$$ae^{-\frac{ax^2}{2}-x}-1>0$$
$$\begin{align*}    (1-x)e^x\geq e^{-\frac{ax^2}{2}}(x\in[0,x_a])     &\Rightarrow\mathop{\underline{\lim}}_{n\to\infty}\sqrt{n}\int_0^1[e^x(1-x)]^n\mathrm{d}x \\     &\geq\mathop{\underline{\lim}}_{n\to\infty}\int_0^{x_a}\sqrt{n}e^{-\frac{nax^2}{2}}\mathrm{d}x\\     &=\sqrt{\frac{\pi}{2a}} \end{align*}$$
因为$a$是任意的，所以
$$\begin{equation*}  \mathop{\underline{\lim}}_{n\to\infty}\sqrt{n}\int_0^1[e^x(1-x)]^n\mathrm{d}x\geq\sqrt{\frac{\pi}{2}} \end{equation*}$$
综上得
$$\begin{equation*}    \lim_{n\to\infty}\sqrt{n}\int_0^1[e^x(1-x)]^n\mathrm{d}x=\sqrt{\frac{\pi}{2}} \end{equation*}$$