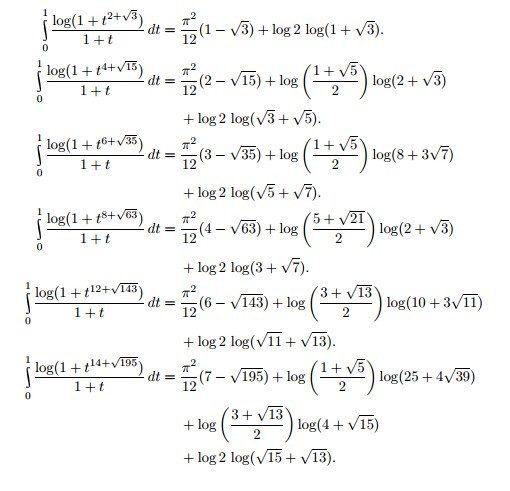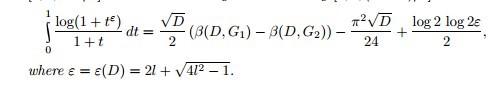设$f(x)$是定义在R上的实函数,且对$\forall x$有$f(x),f'(x),f''(x),f'''(x)>0$,假设对$\forall x$有$f'''(x)<f(x)$证明:对一切$x$都有$f'(x)<2f(x)$.
证明 对任意固定的$c$,令
\[g(x)=f(x)-f'(x)(x-c)+\frac{f''(x)}{2}(x-c)^{2}\]
则
\[ g'(x)=\frac{f'''(x)}{2}(x-c)^{2}\geq 0 \]
所以$g(x)$是递增函数,则对$\forall y>0$
\[ g(c+y)>g(c-y) \]
也就是
\[ g(c+y)=f(c+y)-yf'(c+y)+\frac{f''(c+y)}{2}y^{2}>f(c-y)+yf'(c-y)+\frac{f''(c-y)}{2}y^{2}=g(c-y)\]
注意到
\[ f(c+y)-yf'(c+y)+\frac{f''(c+y)}{2}y^{2}>f(c-y)+yf'(c-y)+\frac{f''(c-y)}{2}y^{2}>\frac{f''(c-y)}{2}y^{2} \]
故有
\[ f(c+y)-yf'(c+y)>\frac{1}{2}y^{2}[f''(c-y)-f''(c+y)] \]
由拉格朗日中值定理知存在$\theta\in(c-y,c+y)$,满足
\[ f''(c+y)-f''(c-y)=2yf'''(\theta)\leq 2yf(\theta)<2yf(c+y) \]
所以
\[ f(c+y)-yf'(c+y)+y^3f(c+y)>0 \]
而由条件可推断
\[\frac{1+y^3}{y}f(c+y)>f'(c+y) \]
当$y=\frac{1}{\sqrt[3]{2}}$上面的$ \frac{1+y^3}{y}=\frac{3}{\sqrt[3]{4}}<2,$
故命题得证。
下面一种证明来着风碎便士同学。
令$c\geq 0$是$f(x)$的下确界,则$f(x)$在$x\rightarrow -\infty$时单调递于$c$,并且容易得到$f'(x),f''(x)$在$x\rightarrow -\infty$时均单调趋于$0$.
这是由于$f''(x)>0$说明$f'(x)$是递增的,故$\displaystyle \lim_{x\rightarrow -\infty}{f'(x)}$要么为$-\infty$,要么为一个常数,而由$\displaystyle \lim_{x\rightarrow -\infty}{f(x)}=c$知,$\displaystyle \lim_{x\rightarrow -\infty}{f'(x)}=0$(其他情况均会矛盾),同样可说明$\displaystyle \lim_{x\rightarrow -\infty}{f''(x)}=0$
从而
\[ f'''(x)f''(x)<f(x)f''(x)<f(x)f''(x)+(f'(x))^2 \]
两边从$a$到$x$积分,得
\[ \frac{1}{2}(f''(x))^2-\frac{1}{2}(f''(a))^2<f(x)f'(x)-f(a)f'(a) \]
再令$a\rightarrow -\infty$得到
\[ (f''(x))^2\leq 2f(x)f'(x) \]
从而
\[ f'''(x)(f''(x))^2\leq 2f^{2}(x)f'(x) \]
两边从$a$到$x$积分,再令$a\rightarrow -\infty$得到
\[ (f''(x))^3\leq 2f^{3}(x) \]
\[ f''(x)\leq \sqrt[3]{2}f(x) \]
\[ f'(x)f''(x) \leq \sqrt[3]{2}f(x)f'(x) \]
两边从$a$到$x$积分,再令$a\rightarrow -\infty$得到
\[ f'(x)\leq \sqrt[6]{2}f(x)<2f(x) \]