Evaluate the following integral
\[ \int_{0}^{\frac{\pi}{2}}\frac{x^2}{1+\cos^2{x}}dx=\frac{\pi}{2\sqrt{2}}\text{Li}_{2}(3-2\sqrt{2})+\frac{\pi^3}{24\sqrt{2}}\]
This integral is deviously difficult. It may look like it has the solution I provided for this integral, but, as you will see, there is an additional wrinkle.
As in the linked solution, I will express the integral in a form in which I may attack via Cauchy’s theorem. I will then deduce the contour over which we will need to apply Cauchy’s theorem – this is the additional wrinkle.
So, to start, let’s rewrite the integral, which I will denote $K$
\[K=\int_0^{\frac{\pi}{2}} \frac{x^2}{1+\cos^2{x}}dx = 2 \int_0^{\frac{\pi}{2}} \frac{x^2}{3+\cos{2 x}}dx = \frac18 \int_{-\pi}^{\pi} \frac{y^2}{3+\cos{y}}dy\]
Along these lines, define
\[J(a) = \int_{-\pi}^{\pi}\frac{e^{i a y}}{3+\cos{y}}dy\]
so that
\[K = -\frac18 J”(0)\]
This then allows us to define the following contour integral
\[I(a) = \oint_C\frac{z^a}{z^2+6 z+1}dz\]
where, as I will explain below, $C$ is the following contour
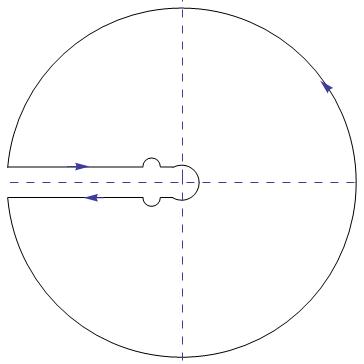
which is a modified keyhole contour about the negative real axis within the unit circle. The modification is a pair of semicircular bumps of radius ϵ about the point $z=-3+2\sqrt{2}$. These bumps are necessary because the integrand has a pole within the unit circle on the chosen branch cut of the integrand (i.e., the negative real axis).
The strategy is to express $I(a)$ in terms of $J(a)$ and other terms, which will then yield an expression for $J(a)$ by Cauchy’s theorem. To do this, we write out $I(a)$ explicitly in terms of integrals along the eight pieces of the contour $C$. This is an exercise in parametrization which is better left to the reader. The result is
\[I(a) = \frac{i}{2} J(a) +e^{i \pi} \int_1^{3-2 \sqrt{2}+\epsilon} \frac{e^{i \pi a} x^a}{x^2-6 x+1}dx \\+ i \epsilon \int_{\pi}^0 \, e^{i \phi} \frac{ [e^{i \pi}(3-2 \sqrt{2})+\epsilon e^{i \phi}]^a}{(-3+2 \sqrt{2}+\epsilon e^{i \phi})^2+6 (-3+2 \sqrt{2}+\epsilon e^{i \phi})+1}d\phi\\ +e^{i \pi} \int_{3-2 \sqrt{2}-\epsilon}^{\epsilon} \frac{e^{i \pi a} x^a}{x^2-6 x+1}dx + i \epsilon \int_{\pi}^{-\pi} e^{i \phi} \frac{\epsilon^a e^{i a \phi}}{\epsilon^2 e^{i 2 \phi}+6 \epsilon e^{i \phi}+1}d\phi \,\\ +e^{-i \pi} \int_{\epsilon}^{3-2 \sqrt{2}-\epsilon} \frac{e^{-i \pi a} x^a}{x^2-6 x+1}dx\\ + i \epsilon \int_0^{-\pi} e^{i \phi} \frac{ [e^{-i \pi}(3-2 \sqrt{2})+\epsilon e^{i \phi}]^a}{(-3+2 \sqrt{2}+\epsilon e^{i \phi})^2+6 (-3+2 \sqrt{2}+\epsilon e^{i \phi})+1} d\phi \, \\+e^{-i \pi} \int_{3-2 \sqrt{2}+\epsilon}^1 \frac{e^{-i \pi a} x^a}{x^2-6 x+1}dx
\]
Actually, one remark is worth making at this point. The parametrization of the semicircular bumps about the point $z=-3+2\sqrt{2}$ requires us to invoke the correct representation of the minus sign. Thus, above the branch cut, $-3+2\sqrt{2}=e^{i\pi}(3-2\sqrt{2})$, while below the branch cut, $-3+2\sqrt{2}=e^{-i\pi}(3-2\sqrt{2})$. This is crucial to the analysis.
We consider the limit as $\epsilon\to 0$; in this limit, the above simplifies considerably:
\[I(a) = \frac{i}{2} J(a) + i 2 \sin{\pi a} \: PV \int_0^1 \frac{x^a}{x^2-6 x+1} – i \frac{\pi}{4 \sqrt{2}} 2 \cos{\pi a} \: (3-2 \sqrt{2})^adx\]
where $PV$ denotes the Cauchy principal value. By Cauchy’s theorem,$I(a)=0;$ this produces an expression for $J(a)$
\[J(a) = \frac{\pi}{\sqrt{2}} \cos{\pi a} \: (3-2 \sqrt{2})^a – 4 \sin{\pi a}\: PV \int_0^1 \frac{x^a}{x^2-6 x+1}dx\]
All we need to do now is use the above expression for $K=-\frac{1}{8}J''(0)$ the result is
\[K = \pi \, PV \int_0^1 \frac{\log{x}}{x^2-6 x+1}dx + \frac{\pi^3}{8 \sqrt{2}} – \frac{\pi}{8 \sqrt{2}} \ln^2{(3-2 \sqrt{2})}\]
To complete this analysis, we evaluate the above integral. Note that it is a principal value, as the integration interval includes a pole of the integrand. To this effect, we note that
\[\frac1{x^2-6 x+1} = \frac1{4 \sqrt{2}} \left (\frac1{x-(3+2 \sqrt{2})} – \frac1{x-(3-2 \sqrt{2})} \right )\]
We use the following formulae, when $b>1$
\[\int_0^1 \frac{\ln{x}}{x-b}dx = \text{Li}_2{\left ( \frac1{b}\right )}\]
and
\[PV:\int_0^1\frac{\ln{x}}{x-\frac{1}{b}}dx =\frac{\pi^2}{3} – \frac12 \ln^2{\left ( \frac1{b}\right )} – \text{Li}_2{\left ( \frac1{b}\right )}\]
Thus, using the value $b=3+2\sqrt{2}$, we find that
\[PV \int_0^1 \frac{\ln{x}}{x^2-6 x+1}dx = \frac1{4 \sqrt{2}} \left [2 \text{Li}_2{(3-2 \sqrt{2})} - \frac{\pi^2}{3} + \frac12 \ln^2{(3-2 \sqrt{2})} \right ]\]
Putting this all together, we find that the $\ln^2$ terms cancel and we have
\[K = \int_0^{\frac{\pi}{2}} \frac{x^2}{1+\cos^2{x}} dx= \frac{\pi}{2 \sqrt{2}} \text{Li}_2{(3-2 \sqrt{2})} + \frac{\pi^3}{24 \sqrt{2}}\]
To summarize, we replaced the $x^2$ in the original integral by a factor of $e^{iay}$, which then became a factor of $z^a$ in a contour integral. The integrand of the contour integral not only has a branch point at $z=0$, but also a pole on the branch cut. The contour of the contour integral then needed to have a detour around this pole on the branch cut. Using Cauchy’s theorem, we got an expression for the integral over $e^{iay}$, and differentiating twice, we got an expression for the original integral in terms of the principal value of another integral. The problem then reduced to evaluating the principal value of that integral.
__________________________________________________________________________________________
是不是被上面的解答吓坏了? 没关系,我发现了个更简单的办法。啊哈哈。。。
\[\int_{0}^{\frac{\pi}{2}}\frac{x^2}{1+\cos^2{x}}dx=\frac{\pi}{2\sqrt{2}}\text{Li}_{2}(3-2\sqrt{2})+\frac{\pi^3}{24\sqrt{2}}\]
注意到
\[ 1+2\sum_{k=1}^{\infty}a^{k}\cos{kx}=\frac{1-a^2}{1-2a\cos{x}+a^2}\qquad |a|<1 \]
所以
\begin{align*}
\int_{0}^{\pi}\frac{x^2}{1-2a\cos{x}+a^2}dx&=\frac{1}{1-a^2}\left(\int_{0}^{\pi}x^2dx+2\int_{0}^{\pi}x^2\sum_{k=1}^{\infty}\cos{kx}dx \right)\\
&=\frac{1}{1-a^2}\left(\frac{\pi^3}{3}+2\sum_{k=1}^{\infty}a^{k}\int_{0}^{\pi}x^2\cos{kx}dx \right)\\
&=\frac{1}{1-a^2}\left(\frac{\pi^3}{3}+2\sum_{k=1}^{\infty}a^{k}\frac{2\pi(-1)^{k}}{k^2}\right)\\
&=\frac{1}{1-a^2}\left(\frac{\pi^3}{3}+4\pi\text{Li}_{2}(-a)\right)
\end{align*}
而
\[ \int_{0}^{\pi}\frac{x^2}{1-2a\cos{x}+a^2}dx=\frac{1}{1+a^2}\int_{0}^{\pi}\frac{x^2}{1-\frac{2a}{1+a^2}\cos{x}}dx\]
\[ \int_{0}^{\frac{\pi}{2}}\frac{x^2}{1+\cos^2{x}}dx=\frac{1}{12}\int_{0}^{\pi}\frac{x^2}{1+\frac{1}{3}\cos{x}}dx \]
于是令
\[ \frac{-2a}{1+a^2}=\frac{1}{3} \qquad |a|<1 \]
得到
\[ a=2\sqrt{2}-3\]
带入,得到
\[\int_{0}^{\frac{\pi}{2}}\frac{x^2}{1+\cos^2{x}}dx=\frac{\pi}{2\sqrt{2}}\text{Li}_{2}(3-2\sqrt{2})+\frac{\pi^3}{24\sqrt{2}}\]
